|
MBDyn-1.7.3
|
|
MBDyn-1.7.3
|
Public Member Functions | |
| asynchronous_machine (unsigned uLabel, const DofOwner *pDO, DataManager *pDM, MBDynParser &HP) | |
| Constructs the element from the information in the input file. More... | |
| virtual | ~asynchronous_machine (void) |
| virtual void | Output (OutputHandler &OH) const |
| Writes private data to a file at each time step. More... | |
| virtual unsigned int | iGetNumDof (void) const |
| The number of private degrees of freedom is determined by this member function. More... | |
| virtual DofOrder::Order | GetDofType (unsigned int i) const |
| The type of the equation of the private degrees of freedom is determined by this member function. More... | |
| virtual std::ostream & | DescribeDof (std::ostream &out, const char *prefix, bool bInitial) const |
| This member function is called if the statement "print: dof description;" is specified in the input file. More... | |
| virtual std::ostream & | DescribeEq (std::ostream &out, const char *prefix, bool bInitial) const |
| This member function is called if the statement "print: equation description;" is specified in the input file. More... | |
| virtual unsigned int | iGetNumPrivData (void) const |
| This member function is called when a bind statement or a element drive is used to access private data of this element. More... | |
| virtual unsigned int | iGetPrivDataIdx (const char *s) const |
| The following string values can be specified in a bind statement or in an element drive caller. More... | |
| virtual doublereal | dGetPrivData (unsigned int i) const |
| This member function is called whenever a bind statement or a element drive is used to access private data. More... | |
| virtual void | SetInitialValue (VectorHandler &X) |
| virtual void | Update (const VectorHandler &XCurr, const VectorHandler &XPrimeCurr) |
| This member function is called after each iteration in the nonlinear solution phase. More... | |
| virtual void | AfterPredict (VectorHandler &X, VectorHandler &XP) |
| virtual void | WorkSpaceDim (integer *piNumRows, integer *piNumCols) const |
| The size of the contribution to the residual and the jacobian matrix is determined by this member function. More... | |
| VariableSubMatrixHandler & | AssJac (VariableSubMatrixHandler &WorkMat, doublereal dCoef, const VectorHandler &XCurr, const VectorHandler &XPrimeCurr) |
Computes the contribution to the jacobian matrix 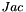 . .More... | |
| SubVectorHandler & | AssRes (SubVectorHandler &WorkVec, doublereal dCoef, const VectorHandler &XCurr, const VectorHandler &XPrimeCurr) |
| This member function implements the equation of an asynchronous machine according to Maschinendynamik Springer 2009, Dresig, Holzweißig. More... | |
| virtual int | iGetNumConnectedNodes (void) const |
| This member function is called if the statement "print: node connection;" is specified in the input file. More... | |
| virtual void | GetConnectedNodes (std::vector< const Node * > &connectedNodes) const |
| This member function is called if the statement "print: node connection;" is specified in the input file. More... | |
| virtual void | SetValue (DataManager *pDM, VectorHandler &X, VectorHandler &XP, SimulationEntity::Hints *ph) |
| This member function is called before the integration starts in order to set the initial values for the private degrees of freedom. More... | |
| virtual std::ostream & | Restart (std::ostream &out) const |
| This member function is called if "make restart file;" is specified in the input file. More... | |
| virtual unsigned int | iGetInitialNumDof (void) const |
| This member function must be implemented only if the initial assembly feature is requested. More... | |
| virtual void | InitialWorkSpaceDim (integer *piNumRows, integer *piNumCols) const |
| virtual VariableSubMatrixHandler & | InitialAssJac (VariableSubMatrixHandler &WorkMat, const VectorHandler &XCurr) |
| virtual SubVectorHandler & | InitialAssRes (SubVectorHandler &WorkVec, const VectorHandler &XCurr) |
 Public Member Functions inherited from Elem Public Member Functions inherited from Elem | |
| Elem (unsigned int uL, flag fOut) | |
| virtual | ~Elem (void) |
| virtual void | DescribeDof (std::vector< std::string > &desc, bool bInitial=false, int i=-1) const |
| virtual void | DescribeEq (std::vector< std::string > &desc, bool bInitial=false, int i=-1) const |
| virtual void | AssMats (VariableSubMatrixHandler &WorkMatA, VariableSubMatrixHandler &WorkMatB, const VectorHandler &XCurr, const VectorHandler &XPrimeCurr) |
| virtual bool | bInverseDynamics (void) const |
| void | SetInverseDynamicsFlags (unsigned uIDF) |
| unsigned | GetInverseDynamicsFlags (void) const |
| bool | bIsErgonomy (void) const |
| bool | bIsRightHandSide (void) const |
| virtual VariableSubMatrixHandler & | AssJac (VariableSubMatrixHandler &WorkMat, const VectorHandler &XCurr) |
| virtual SubVectorHandler & | AssRes (SubVectorHandler &WorkVec, const VectorHandler &XCurr, const VectorHandler &XPrimeCurr, const VectorHandler &XPrimePrimeCurr, InverseDynamics::Order iOrder=InverseDynamics::INVERSE_DYNAMICS) |
| virtual int | GetNumConnectedNodes (void) const |
 Public Member Functions inherited from WithLabel Public Member Functions inherited from WithLabel | |
| WithLabel (unsigned int uL=0, const std::string &sN="") | |
| virtual | ~WithLabel (void) |
| void | PutLabel (unsigned int uL) |
| void | PutName (const std::string &sN) |
| unsigned int | GetLabel (void) const |
| const std::string & | GetName (void) const |
 Public Member Functions inherited from SimulationEntity Public Member Functions inherited from SimulationEntity | |
| SimulationEntity (void) | |
| virtual | ~SimulationEntity (void) |
| virtual bool | bIsValidIndex (unsigned int i) const |
| virtual DofOrder::Order | GetEqType (unsigned int i) const |
| virtual Hint * | ParseHint (DataManager *pDM, const char *s) const |
| virtual void | BeforePredict (VectorHandler &, VectorHandler &, VectorHandler &, VectorHandler &) const |
| virtual void | DerivativesUpdate (const VectorHandler &XCurr, const VectorHandler &XPrimeCurr) |
| virtual void | Update (const VectorHandler &XCurr, InverseDynamics::Order iOrder) |
| virtual void | AfterConvergence (const VectorHandler &X, const VectorHandler &XP) |
| virtual void | AfterConvergence (const VectorHandler &X, const VectorHandler &XP, const VectorHandler &XPP) |
| virtual std::ostream & | OutputAppend (std::ostream &out) const |
| virtual void | ReadInitialState (MBDynParser &HP) |
 Public Member Functions inherited from ToBeOutput Public Member Functions inherited from ToBeOutput | |
| ToBeOutput (flag fOut=fDefaultOut) | |
| virtual | ~ToBeOutput (void) |
| virtual void | OutputPrepare (OutputHandler &OH) |
| virtual void | Output (OutputHandler &OH, const VectorHandler &X, const VectorHandler &XP) const |
| virtual flag | fToBeOutput (void) const |
| virtual bool | bToBeOutput (void) const |
| virtual void | SetOutputFlag (flag f=flag(1)) |
 Public Member Functions inherited from UserDefinedElem Public Member Functions inherited from UserDefinedElem | |
| UserDefinedElem (unsigned uLabel, const DofOwner *pDO) | |
| virtual | ~UserDefinedElem (void) |
| bool | NeedsAirProperties (void) const |
| void | NeedsAirProperties (bool yesno) |
| virtual Elem::Type | GetElemType (void) const |
| virtual AerodynamicElem::Type | GetAerodynamicElemType (void) const |
 Public Member Functions inherited from InitialAssemblyElem Public Member Functions inherited from InitialAssemblyElem | |
| InitialAssemblyElem (unsigned int uL, flag fOut) | |
| virtual | ~InitialAssemblyElem (void) |
 Public Member Functions inherited from SubjectToInitialAssembly Public Member Functions inherited from SubjectToInitialAssembly | |
| SubjectToInitialAssembly (void) | |
| virtual | ~SubjectToInitialAssembly (void) |
 Public Member Functions inherited from AerodynamicElem Public Member Functions inherited from AerodynamicElem | |
| AerodynamicElem (unsigned int uL, const DofOwner *pDO, flag fOut) | |
| virtual | ~AerodynamicElem (void) |
| virtual const InducedVelocity * | pGetInducedVelocity (void) const |
 Public Member Functions inherited from ElemWithDofs Public Member Functions inherited from ElemWithDofs | |
| ElemWithDofs (unsigned int uL, const DofOwner *pDO, flag fOut) | |
| virtual | ~ElemWithDofs (void) |
 Public Member Functions inherited from DofOwnerOwner Public Member Functions inherited from DofOwnerOwner | |
| DofOwnerOwner (const DofOwner *pDO) | |
| virtual | ~DofOwnerOwner () |
| virtual const DofOwner * | pGetDofOwner (void) const |
| virtual integer | iGetFirstIndex (void) const |
 Public Member Functions inherited from AirPropOwner Public Member Functions inherited from AirPropOwner | |
| AirPropOwner (void) | |
| virtual | ~AirPropOwner (void) |
| virtual void | PutAirProperties (const AirProperties *pAP) |
| virtual flag | fGetAirVelocity (Vec3 &Velocity, const Vec3 &X) const |
| virtual doublereal | dGetAirDensity (const Vec3 &X) const |
| virtual doublereal | dGetAirPressure (const Vec3 &X) const |
| virtual doublereal | dGetAirTemperature (const Vec3 &X) const |
| virtual doublereal | dGetSoundSpeed (const Vec3 &X) const |
| virtual bool | GetAirProps (const Vec3 &X, doublereal &rho, doublereal &c, doublereal &p, doublereal &T) const |
 Public Member Functions inherited from ElemGravityOwner Public Member Functions inherited from ElemGravityOwner | |
| ElemGravityOwner (unsigned int uL, flag fOut) | |
| virtual | ~ElemGravityOwner (void) |
| virtual doublereal | dGetM (void) const |
| Vec3 | GetS (void) const |
| Mat3x3 | GetJ (void) const |
| Vec3 | GetB (void) const |
| Vec3 | GetG (void) const |
 Public Member Functions inherited from GravityOwner Public Member Functions inherited from GravityOwner | |
| GravityOwner (void) | |
| virtual | ~GravityOwner (void) |
| void | PutGravity (const Gravity *pG) |
| virtual bool | bGetGravity (const Vec3 &X, Vec3 &Acc) const |
Private Member Functions | |
| bool | IsMotorOn (void) const |
| If a drive caller has been specified in the input file the value returned by the drive caller is used to determine if the motor is powered on. If no drive caller has been specified in the input file it is assumed that the motor is always powered on. More... | |
Private Attributes | |
| const StructNode * | m_pRotorNode |
| const StructNode * | m_pStatorNode |
| doublereal | m_MK |
| doublereal | m_sK |
| DriveOwner | m_OmegaS |
| DriveOwner | m_MotorOn |
| doublereal | m_M |
| doublereal | m_dM_dt |
| doublereal | m_dM_dt2 |
| doublereal | m_omega |
| doublereal | m_domega_dt |
Static Private Attributes | |
| static const doublereal | sm_SingTol = std::pow(std::numeric_limits<doublereal>::epsilon(), 0.9) |
This code is a simple example on how to implement a user defined element for the free multibody software MBDyn. Since no documentation exists for user defined elements in MBDyn at the time of writing I have written this document in the hope that it will be helpful for others who want to write their own user defined elements for MBDyn.
The purpose of this code is the simulation of an asynchronous electrical machine as a part of a multibody model. With this software the coupling between the mechanical and the electrical differential equations can be considered. The theoretical background is based on the book Maschinendynamik Springer 2009, Dresig, Holzweißig.
In the formulas in this book the stator resistance is neglected and the free run slip is assumed to be zero. Also small perturbations around the mean angular velocity are assumed.
The input parameters for the simulation are:
Breakdown torque 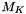 .
.
Slip at the breakdown torque 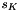 .
.
Synchronous angular velocity 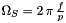 (might be a function of the time in case of an frequency inverter).
(might be a function of the time in case of an frequency inverter).
A flag that determines whether the power supply is turned on or off 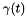 .
.
Optional the initial value of the motor torque 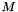 .
.
Optional the initial value of the first derivative of the motor torque 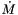 .
.
The sense of rotation is determined by the sign of 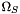 . If the sign is positive, the sense of rotation is also positive in the reference frame of the stator node.
. If the sign is positive, the sense of rotation is also positive in the reference frame of the stator node.
This code is implemented as an user defined element for MBDyn. The element is connected to two structural nodes. The rotor node and the stator node. The axis of rotation is assumed to be axis three in the reference frame of the stator node. It is assumed that the axis of the rotor node is parallel to the axis of the stator node. The torque is imposed to the structural nodes in direction of axis three in the reference frame of the stator node. The synchronous angular velocity can be specified by means of a drive caller. This allows to simulate a frequency inverter.
Definition at line 84 of file module-asynchronous_machine.cc.
| asynchronous_machine::asynchronous_machine | ( | unsigned | uLabel, |
| const DofOwner * | pDO, | ||
| DataManager * | pDM, | ||
| MBDynParser & | HP | ||
| ) |
Constructs the element from the information in the input file.
| uLabel | the label assigned to this element in the input file |
| pDO | |
| pDM | pointer to the data manager (needed to read structural nodes for example) |
| HP | reference to the math parser (needed to read from the input file) A description of the exact input file syntax can be retrieved by adding the following statement to the MBDyn input file: user defined: 1, asynchronous_machine, help; |
Definition at line 157 of file module-asynchronous_machine.cc.
References copysign(), DriveOwner::dGet(), DataManager::fReadOutput(), Mat3x3::GetCol(), MBDynParser::GetDriveCaller(), WithLabel::GetLabel(), IncludeParser::GetLineData(), DataManager::GetLogFile(), StructNode::GetRCurr(), HighParser::GetReal(), StructNode::GetWCurr(), HighParser::IsArg(), HighParser::IsKeyWord(), IsMotorOn(), Elem::LOADABLE, m_dM_dt, m_dM_dt2, m_M, m_MK, m_MotorOn, m_omega, m_OmegaS, m_pRotorNode, m_pStatorNode, m_sK, MBDYN_EXCEPT_ARGS, DataManager::ReadNode(), DriveOwner::Set(), ToBeOutput::SetOutputFlag(), and Node::STRUCTURAL.
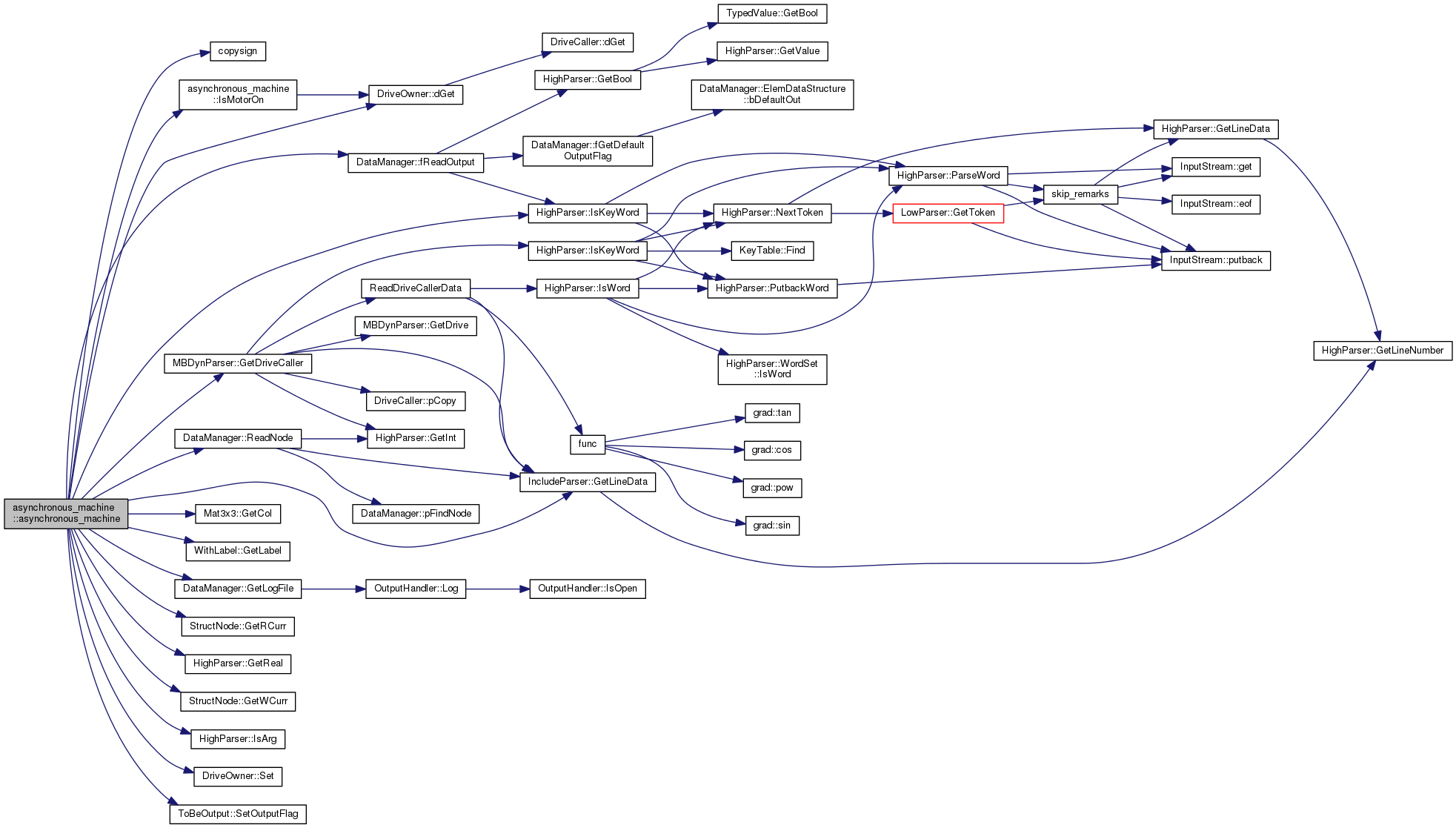
|
virtual |
Definition at line 343 of file module-asynchronous_machine.cc.
|
virtual |
Reimplemented from SimulationEntity.
Definition at line 327 of file module-asynchronous_machine.cc.
References Update().

|
virtual |
Computes the contribution to the jacobian matrix 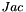 .
.
| WorkMat | sparse or full submatrix which receives the contribution to the jacobian matrix 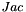 |
| dCoef | the derivative coefficient is defined as 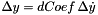 |
| XCurr | the vector of the global degrees of freedom 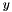 at the current iteration step at the current iteration step |
| XPrimeCurr | the vector of the derivative of the global degrees of freedom 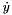
For the definition of 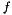 see AssRes(). see AssRes().
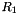 is the corrected rotation matrix of node 1 at the current iteration which can be obtained by GetRCurr(). is the corrected rotation matrix of node 1 at the current iteration which can be obtained by GetRCurr().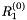 is the predicted rotation matrix of node 1 at the current time step which can be obtained by GetRRef(). is the predicted rotation matrix of node 1 at the current time step which can be obtained by GetRRef().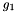 is the vector of Gibbs Rodriguez rotation parameters of node 1. is the vector of Gibbs Rodriguez rotation parameters of node 1.The rotation matrix 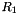 is internally computed as follows: is internally computed as follows:
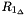 is the incremental rotation matrix which can be computed by means of the Gibbs Rodriguez rotation parameters is the incremental rotation matrix which can be computed by means of the Gibbs Rodriguez rotation parameters 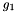 . .
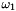 is the corrected angular velocity of node 1 at the current iteration which can be obtained by GetWCurr(). is the corrected angular velocity of node 1 at the current iteration which can be obtained by GetWCurr().
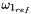 is the predicted angular velocity of node 1 at the current time step which can be obtained by GetWRef(). is the predicted angular velocity of node 1 at the current time step which can be obtained by GetWRef().
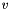 is a const vector in the reference frame is a const vector in the reference frame 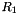 . .
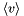 is a matrix that rearranges the components of is a matrix that rearranges the components of 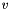 according to the cross product rule: according to the cross product rule: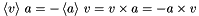
|
Implements Elem.
Definition at line 627 of file module-asynchronous_machine.cc.
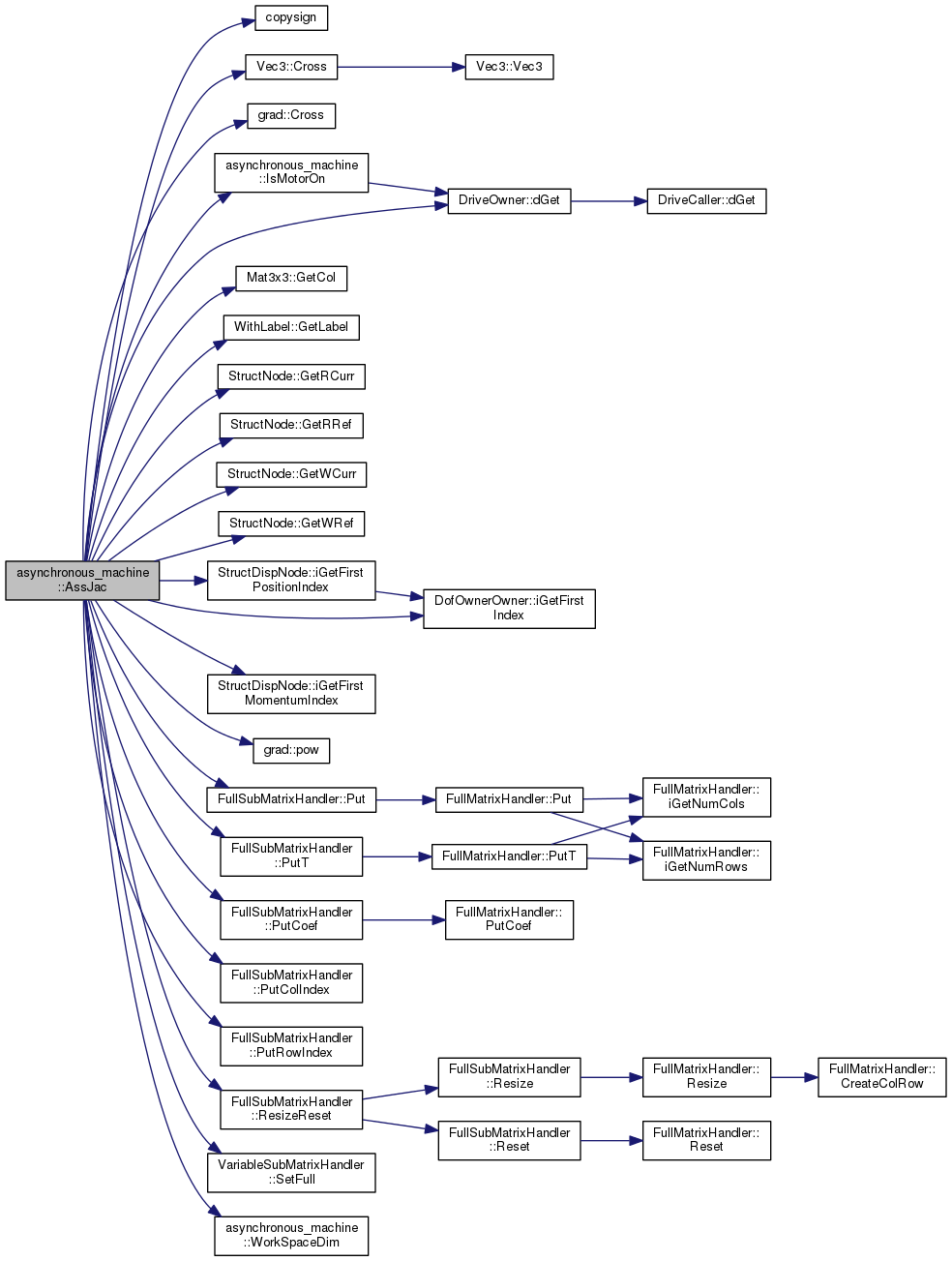
References copysign(), Vec3::Cross(), grad::Cross(), DriveOwner::dGet(), Mat3x3::GetCol(), WithLabel::GetLabel(), StructNode::GetRCurr(), StructNode::GetRRef(), StructNode::GetWCurr(), StructNode::GetWRef(), DofOwnerOwner::iGetFirstIndex(), StructDispNode::iGetFirstMomentumIndex(), StructDispNode::iGetFirstPositionIndex(), IsMotorOn(), m_MK, m_OmegaS, m_pRotorNode, m_pStatorNode, m_sK, MatCross, grad::pow(), FullSubMatrixHandler::Put(), FullSubMatrixHandler::PutCoef(), FullSubMatrixHandler::PutColIndex(), FullSubMatrixHandler::PutRowIndex(), FullSubMatrixHandler::PutT(), FullSubMatrixHandler::ResizeReset(), VariableSubMatrixHandler::SetFull(), sm_SingTol, and WorkSpaceDim().
|
virtual |
This member function implements the equation of an asynchronous machine according to Maschinendynamik Springer 2009, Dresig, Holzweißig.
| WorkVec | subvector which receives the contribution to the residual 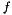 |
| dCoef | the derivative coefficient is defined as 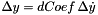 |
| XCurr | the vector of the global degrees of freedom 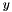 at the current iteration step at the current iteration step |
| XPrimeCurr | the vector of the derivative of the global degrees of freedom 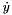
The term 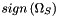 and the absolute operator in and the absolute operator in 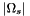 are modifications of the original formula since the formula in the literature does not handle negative synchronous angular velocities are modifications of the original formula since the formula in the literature does not handle negative synchronous angular velocities 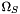 . If the synchronous angular velocity . If the synchronous angular velocity 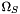 has a negative value, the sense of rotation is assumed to be negative. has a negative value, the sense of rotation is assumed to be negative.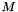 is motor torque is motor torque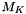 is the breakdown torque is the breakdown torque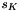 is the breakdown slip is the breakdown slip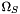 is the synchronous angular velocity of the machine is the synchronous angular velocity of the machine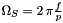 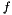 is the power frequency is the power frequency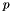 is the number of terminal pairs is the number of terminal pairs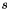 is the actual slip is the actual slip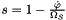 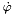 is the relative angular velocity of the rotor with respect to the stator is the relative angular velocity of the rotor with respect to the statorThe axis of rotation is assumed to be axis 3 in the reference frame of the stator node. 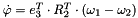 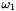 is the angular velocity of the rotor node in the global reference frame which can be obtained by GetWCurr() is the angular velocity of the rotor node in the global reference frame which can be obtained by GetWCurr()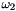 is the angular velocity of the stator node in the global reference frame is the angular velocity of the stator node in the global reference frame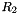 is the rotation matrix of the stator node which can be obtained by GetRCurr() is the rotation matrix of the stator node which can be obtained by GetRCurr()The subvector of the global degrees of freedom XCurr used by this element is
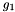 is the vector of rotation parameters of the rotor node. is the vector of rotation parameters of the rotor node.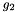 is the vector of the rotation parameters of the stator node. is the vector of the rotation parameters of the stator node.The index of 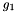 and and 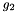 can be obtained by iGetFirstMomentumIndex() + 4 ... 6. can be obtained by iGetFirstMomentumIndex() + 4 ... 6.The index of 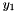 , , 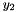 and and 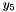 in the vector of the global degrees of freedom XCurr can be obtained by iGetFirstIndex() + 1 ... 3. in the vector of the global degrees of freedom XCurr can be obtained by iGetFirstIndex() + 1 ... 3.The subvector of the derivatives of the global degrees of freedom used by this element is
The additional degree of freedom 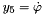 is needed since MBDyn does not provide the angular acceleration of a node during the nonlinear solution phase. The value returned by GetWPCurr() is updated only after convergence and can not be used for this reason. The contribution to the residual of this element is is needed since MBDyn does not provide the angular acceleration of a node during the nonlinear solution phase. The value returned by GetWPCurr() is updated only after convergence and can not be used for this reason. The contribution to the residual of this element is
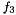 is the torque imposed to the rotor node. is the torque imposed to the rotor node.
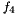 is the torque imposed to the stator node. is the torque imposed to the stator node.
|
Implements Elem.
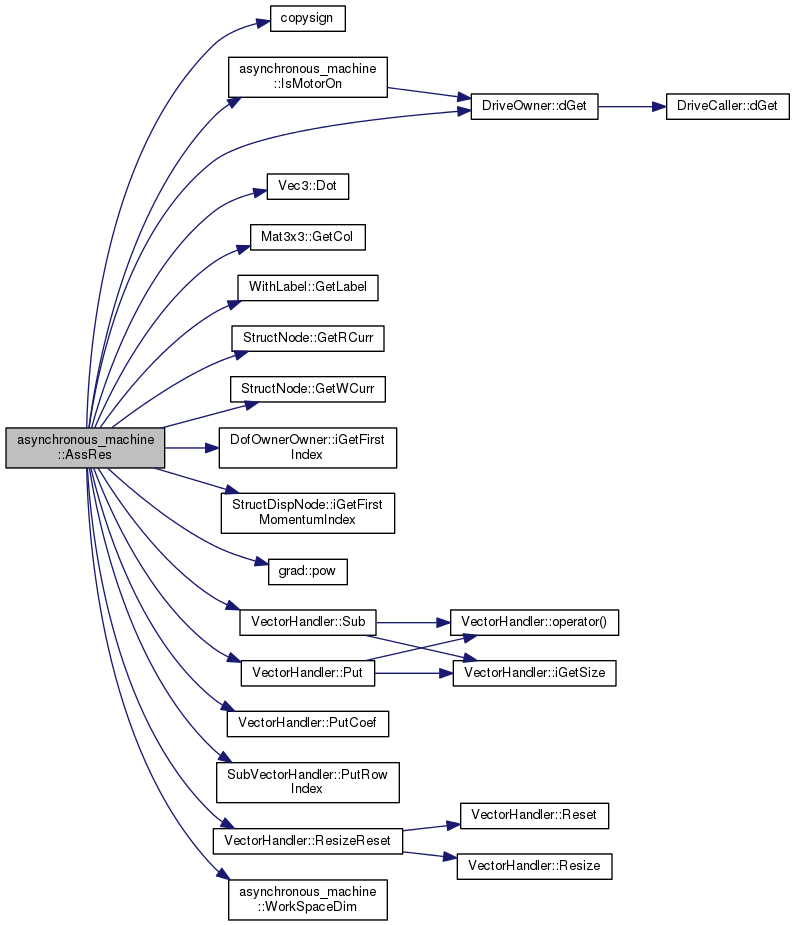
Definition at line 871 of file module-asynchronous_machine.cc.
References copysign(), DriveOwner::dGet(), Vec3::Dot(), Mat3x3::GetCol(), WithLabel::GetLabel(), StructNode::GetRCurr(), StructNode::GetWCurr(), DofOwnerOwner::iGetFirstIndex(), StructDispNode::iGetFirstMomentumIndex(), IsMotorOn(), m_MK, m_OmegaS, m_pRotorNode, m_pStatorNode, m_sK, grad::pow(), VectorHandler::Put(), VectorHandler::PutCoef(), SubVectorHandler::PutRowIndex(), VectorHandler::ResizeReset(), sm_SingTol, VectorHandler::Sub(), and WorkSpaceDim().
|
virtual |
This member function is called if the statement "print: dof description;" is specified in the input file.
| out | output stream that receives the formated output |
| prefix | should be output in the first column |
It prints a short description of the private degrees of freedom 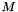 ,
, 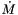 and
and 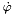 .
.
Reimplemented from Elem.
Definition at line 452 of file module-asynchronous_machine.cc.
References DofOwnerOwner::iGetFirstIndex().

|
virtual |
This member function is called if the statement "print: equation description;" is specified in the input file.
| out | output stream that receives the formated output |
| prefix | should be output in the first column |
It prints a short description of the residual of the private degrees of freedom 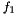 ,
, 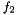 and
and 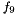 .
.
Reimplemented from Elem.
Definition at line 473 of file module-asynchronous_machine.cc.
References DofOwnerOwner::iGetFirstIndex().

|
virtual |
This member function is called whenever a bind statement or a element drive is used to access private data.
| i | the one based index of the private data |
Reimplemented from SimulationEntity.
Definition at line 544 of file module-asynchronous_machine.cc.
References copysign(), DriveOwner::dGet(), m_dM_dt, m_dM_dt2, m_domega_dt, m_M, m_omega, m_OmegaS, and MBDYN_EXCEPT_ARGS.

|
virtual |
This member function is called if the statement "print: node connection;" is specified in the input file.
| connectedNodes | vector which receives pointers to the connected nodes |
Reimplemented from Elem.
Definition at line 987 of file module-asynchronous_machine.cc.
References iGetNumConnectedNodes(), m_pRotorNode, and m_pStatorNode.

|
virtual |
The type of the equation of the private degrees of freedom is determined by this member function.
| i | zero based index of the private degree of freedom (zero for the first private degree of freedom, one for second ...) |
Reimplemented from Elem.
Definition at line 437 of file module-asynchronous_machine.cc.
References DofOrder::DIFFERENTIAL.
|
virtual |
This member function must be implemented only if the initial assembly feature is requested.
The initial assembly phase is needed only if initial values are provided which are not consistent with the algebraic constraints. Since this element does not use algebraic constraints we do not have to implement iGetInitialNumDof(), InitialWorkSpaceDim(), InitialAssJac(), InitialAssRes() and SetInitialValue().
Implements SubjectToInitialAssembly.
Definition at line 1046 of file module-asynchronous_machine.cc.
|
virtual |
This member function is called if the statement "print: node connection;" is specified in the input file.
Definition at line 977 of file module-asynchronous_machine.cc.
Referenced by GetConnectedNodes().
|
virtual |
The number of private degrees of freedom is determined by this member function.
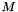 ,
, 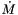 and
and 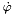 are private degrees of freedom only accessible to this element.
are private degrees of freedom only accessible to this element. Reimplemented from Elem.
Definition at line 426 of file module-asynchronous_machine.cc.
|
virtual |
This member function is called when a bind statement or a element drive is used to access private data of this element.
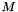 ,
, 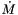 ,
, 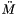 ,
, 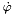 and
and 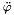 are available.
are available. Reimplemented from SimulationEntity.
Definition at line 492 of file module-asynchronous_machine.cc.
|
virtual |
The following string values can be specified in a bind statement or in an element drive caller.
| s | specifies the name of the private data to be accessed by a bind statement or an element drive caller. |
| index | string | variable |
| 1 | M | 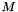 |
| 2 | MP | 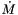 |
| 3 | MPP | 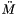 |
| 4 | omega | 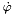 |
| 5 | omegaP | 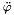 |
Reimplemented from SimulationEntity.
Definition at line 512 of file module-asynchronous_machine.cc.
References WithLabel::GetLabel().

|
virtual |
See iGetInitialNumDof().
Implements SubjectToInitialAssembly.
Definition at line 1067 of file module-asynchronous_machine.cc.
References VariableSubMatrixHandler::SetNullMatrix().

|
virtual |
See iGetInitialNumDof().
Implements SubjectToInitialAssembly.
Definition at line 1080 of file module-asynchronous_machine.cc.
References VectorHandler::ResizeReset().

|
virtual |
See iGetInitialNumDof().
Implements SubjectToInitialAssembly.
Definition at line 1055 of file module-asynchronous_machine.cc.
|
private |
If a drive caller has been specified in the input file the value returned by the drive caller is used to determine if the motor is powered on. If no drive caller has been specified in the input file it is assumed that the motor is always powered on.
Definition at line 338 of file module-asynchronous_machine.cc.
References DriveOwner::dGet(), and m_MotorOn.
Referenced by AssJac(), AssRes(), asynchronous_machine(), and Output().

|
virtual |
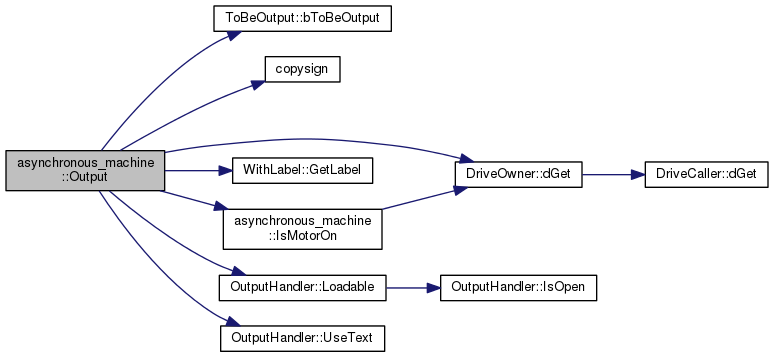
Writes private data to a file at each time step.
| OH | OH.Loadable() returns a reference to the stream intended for the output of loadable elements. The output format is as follows:
|
Reimplemented from ToBeOutput.
Definition at line 370 of file module-asynchronous_machine.cc.
References ToBeOutput::bToBeOutput(), copysign(), DriveOwner::dGet(), WithLabel::GetLabel(), IsMotorOn(), OutputHandler::LOADABLE, OutputHandler::Loadable(), m_dM_dt, m_dM_dt2, m_domega_dt, m_M, m_omega, m_OmegaS, and OutputHandler::UseText().
|
virtual |
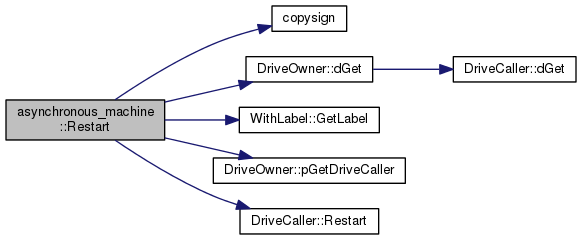
This member function is called if "make restart file;" is specified in the input file.
| out | stream of the restart file It should reproduce the syntax in the input file used to create this element. |
Implements Elem.
Definition at line 1020 of file module-asynchronous_machine.cc.
References copysign(), DriveOwner::dGet(), WithLabel::GetLabel(), m_dM_dt, m_M, m_MK, m_MotorOn, m_OmegaS, m_pRotorNode, m_pStatorNode, m_sK, DriveOwner::pGetDriveCaller(), and DriveCaller::Restart().
|
virtual |
See iGetInitialNumDof().
Reimplemented from DofOwnerOwner.
Definition at line 572 of file module-asynchronous_machine.cc.
|
virtual |
This member function is called before the integration starts in order to set the initial values for the private degrees of freedom.
| X | vector of global degrees of freedom 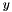 that receives the initial values provided by this element. that receives the initial values provided by this element. |
| XP | vector of the derivative of the global degrees of freedom 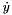 In our case the initial values for In our case the initial values for 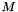 , , 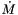 and and 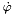 are set in this routine to the values specified in the input file. are set in this routine to the values specified in the input file. |
Reimplemented from SimulationEntity.
Definition at line 1002 of file module-asynchronous_machine.cc.
References DofOwnerOwner::iGetFirstIndex(), m_dM_dt, m_M, m_omega, and VectorHandler::Put().
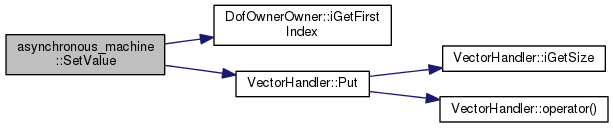
|
virtual |
This member function is called after each iteration in the nonlinear solution phase.
| X | vector of global degrees of freedom 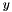 after convergence at the current time step. after convergence at the current time step. |
| XP | derivative of the global degrees of freedom 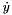 after convergence at the current time step. after convergence at the current time step.In our element this member function saves the current state of the private degrees of freedom. This is needed for the implementation of the Output() and the dGetPrivData() member functions. If the private degrees of freedom are needed just for Output(), the code that saves it's state should be moved to AfterPredict() since this member function is called only once per time step. |
Reimplemented from SimulationEntity.
Definition at line 311 of file module-asynchronous_machine.cc.
References DofOwnerOwner::iGetFirstIndex(), m_dM_dt, m_dM_dt2, m_domega_dt, m_M, and m_omega.
Referenced by AfterPredict().

The size of the contribution to the residual and the jacobian matrix is determined by this member function.
| piNumRows | pointer to a variable which receives the number of rows of the contribution to the residual vector and the jacobian matrix |
| piNumCols | pointer to a variable which receives the number of columns of the contribution to the jacobian matrix |
Implements Elem.
Definition at line 415 of file module-asynchronous_machine.cc.
|
private |
holds the first derivative of the motor torque 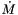 after convergence
after convergence
Definition at line 138 of file module-asynchronous_machine.cc.
Referenced by asynchronous_machine(), dGetPrivData(), Output(), Restart(), SetValue(), and Update().
|
private |
holds the second derivative of the motor torque 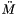 after convergence
after convergence
Definition at line 139 of file module-asynchronous_machine.cc.
Referenced by asynchronous_machine(), dGetPrivData(), Output(), and Update().
|
private |
holds the angular acceleration 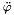 of the rotor node relative to the stator node after convergence
of the rotor node relative to the stator node after convergence
Definition at line 141 of file module-asynchronous_machine.cc.
Referenced by dGetPrivData(), Output(), and Update().
|
private |
holds the motor torque 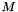 after convergence for convenience
after convergence for convenience
Definition at line 137 of file module-asynchronous_machine.cc.
Referenced by asynchronous_machine(), dGetPrivData(), Output(), Restart(), SetValue(), and Update().
|
private |
breakdown torque 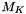
Definition at line 133 of file module-asynchronous_machine.cc.
Referenced by AssJac(), AssRes(), asynchronous_machine(), and Restart().
|
private |
drive that returns whether the power supply is turned on or off 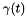
Definition at line 136 of file module-asynchronous_machine.cc.
Referenced by asynchronous_machine(), IsMotorOn(), and Restart().
|
private |
holds the angular velocity 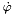 of the rotor relative to the stator around axis 3 of the stator node after convergence
of the rotor relative to the stator around axis 3 of the stator node after convergence
Definition at line 140 of file module-asynchronous_machine.cc.
Referenced by asynchronous_machine(), dGetPrivData(), Output(), SetValue(), and Update().
|
private |
drive that returns the synchronous angular velocity 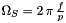 (might be a function of the time in case of an frequency inverter)
(might be a function of the time in case of an frequency inverter)
Definition at line 135 of file module-asynchronous_machine.cc.
Referenced by AssJac(), AssRes(), asynchronous_machine(), dGetPrivData(), Output(), and Restart().
|
private |
node of the rotor where the torque 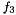 is imposed and the angular velocity
is imposed and the angular velocity 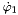 is determined
is determined
Definition at line 131 of file module-asynchronous_machine.cc.
Referenced by AssJac(), AssRes(), asynchronous_machine(), GetConnectedNodes(), and Restart().
|
private |
node of the stator where the torque 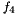 is applied and the angular velocity
is applied and the angular velocity 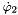 is determined (axis 3 of the stator node is assumed to be the axis of rotation)
is determined (axis 3 of the stator node is assumed to be the axis of rotation)
Definition at line 132 of file module-asynchronous_machine.cc.
Referenced by AssJac(), AssRes(), asynchronous_machine(), GetConnectedNodes(), and Restart().
|
private |
slip at the breakdown torque 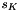
Definition at line 134 of file module-asynchronous_machine.cc.
Referenced by AssJac(), AssRes(), asynchronous_machine(), and Restart().
|
staticprivate |
Definition at line 142 of file module-asynchronous_machine.cc.